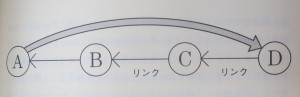
･･･人間というのは実際には、Aというのを聞いた途端にDという結論を出してしまうんだ。根拠なしに、いきなり飛んじまう。
･･･要するに、順番が逆なわけ。形式論理が言うA→B→C→Dという順序は、後付けなんだ。後付けにもかかわらず、さもそういう順序で導かれるようなことを言っている。･･･Aと聞いたら、頭の中ではいきなりDに飛んで行ってしまうんだ。それから、ウラでこっそりD→C→B→Aと逆から組み立てて、論理のつながりが確認できたところでひっくり返してんだよ。
それから、何食わぬ顔をして「A→B→C→Dですね」なんて言っているだけなの。まったくズルイんだ。数学の先生は、こういうウラ事情を絶対明かさない。･･･
※直観でわかる数学、畑村洋太郎著、岩波書店、2004年、188-190頁、引用
数学は説明する学問
数学をなぜ勉強するのか？ このいやらしい（？）命題に対し、たぶん答えのひとつとして「数学は誰か（何か）に説明する学問だ」というのがあると思う。つまり、数学は “説明する学問” だと思う。
畑村洋太郎先生（工学院大学教授・東京大学名誉教授）の『直観でわかる数学
つまり、人間は日常生活で、まず①A→Dのような直感的に結論をくだす。そして、②D→C→B→Aのように逆算して考える。最後に③A→B→C→Dと順を追って考える。
さらに言えば、その「A→B→C→D」の順番で、他の人やコンピューターに “説明” すると、その人やコンピューター（プログラム）も “納得” してくれる。納得して、そのように動いてくれる。そのように考えて行動してくれる。
たとえば、朝寝坊したとする。パッと起きた瞬間、①時計を見て「遅刻だ！」と悟る。②学校から通学経路を逆算して、どこかで時間短縮できないか必死に考える。そして、いつものバス通学をバイクに切り替え、駅の有料バイク駐輪スペースに留めることを思いつく。③最後に、自宅→バイク→駐輪場→駅と、経路を順を追ってイメージする。
それで、家族がもし何かの用事で遅刻しそうになったら、③「自宅→バイク→駐輪場→駅」の順序で説明する。そうすると、その家族は納得し、急いでバイクに乗って駅に（駅の駐輪場に）向かうのである。
数学で人々を操作できる
で、数学はこの最後の③「A→B→C→D」を学ぶ教科です。だから、数学は物事を説明・解説するのには都合がいいが、日常生活の発想手順の最後に来る部分だけあって、なかなかなじめない。直感的でない。多くの人は普段そう考えないし、逆に普段から数学的に発想する人は “理屈っぽい” と敬遠される。
だから数学は嫌われる。しかし、数学をうまく使えば、（極端に言えば）人々やコンピューターを自在に操れる。「A→B→C→D」を自分で理解し、人やマシンに “解説” すれば、人間の行動様式や機械のプログラムを書き換えることができる。
だから、世界中の教育機関・公共教育には「数学」は必ずあるし、人間社会のあらゆる “裏側” で「数学」が息づいている。見えないところであるが「数学」が森羅万象のバックグラウンドで生きているから、人々もコンピューターも無意識に本能的に納得して（？）動かされる。
つまり、みんなが嫌う数学を習得すると、みんなが気がつかないところで、みんなを “操作” することができる。まぁでも、こんな発想は、僕の好きな数学講師の佐藤充先生（秀英iD予備校）に言わせれば、完全に邪道な考えかもしれませんが･･･。彼はプチ体育会系というか「直球勝負の正統派教師」ですから。
いずれにせよ、この数学の意外な “操作性”（？）が数学を学ぶ（陰の）理由だと思う。もしかして、とりわけ「数学」は（他の生物に比べ）知的な社会生活を送る人間にだけに神が与えた学問なのかもしれません。
※参考資料：
・畑村洋太郎、Wikipedia、最終更新2015年03月21日
・プログラム (コンピュータ)、Wikipedia、最終更新2014年08月15日
・中学講座｜ネット学習塾｜実力の教師陣、秀英ｉＤ予備校